Avoidable Rectangle

Eine Situation in einem eindeutigen Sudoku, bei dem zwei Kandidaten 'A' und 'B' in VIER rechteckförmig angeordneten Zellen genau ZWEI Zeilen und ZWEI Spalten und ZWEI Blöcke belegt, ist unmöglich:

      AB - AB
      |     |
      AB - AB

  Hier zeigen die grünen Zellen ein gültiges Muster in einem eindeutigen Sudoku (da 2 Zeilen und 2 Spalten und 4 Blöcke!),
  die roten Zellen dagegen ein unmögliches Muster ("deadly pattern") mit 2 Zeilen und 2 Spalten und 2 Blöcke:

   

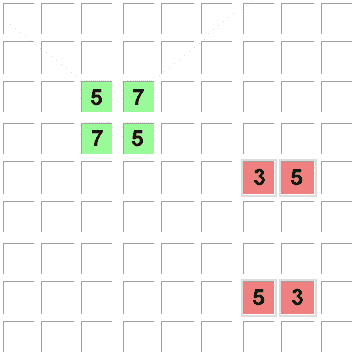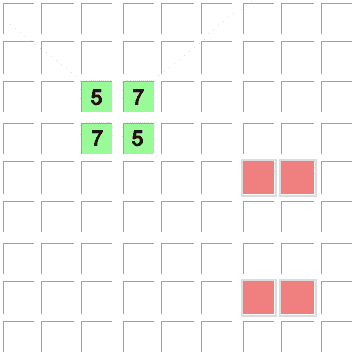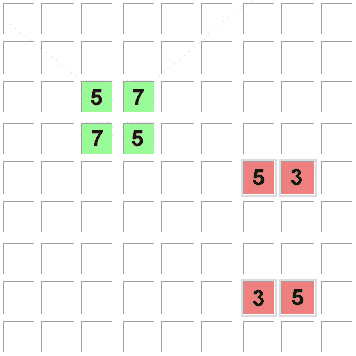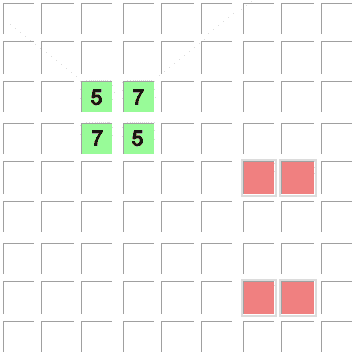
Bei diesem unmöglichen Muster ("deadly pattern") würde sich ein Sudoku mit 2 Lösungen (also KEIN eindeutiges mit nur EINER Lösung) ergeben,
da die Kandidaten 'A' und 'B' untereinander austauschbar wären:

      A - B               B - A
      |   |     oder      |   |
      B - A               A - B

Daraus abgeleitet, wurde die Lösungstechnik 'Avoidable Rectangle' ('Vermeidbares Rechteck') entwickelt,
die auf dem Ausschluss der Zweilösungs-Situation basiert:

Voraussetzungen für 'Avoidable Rectangle':

• ein eindeutiges Sudoku mit nur einer Lösung;
• VIER rechteckförmig angeordnete Zellen mit Kandidaten 'A' und 'B' belegen genau ZWEI Zeilen und ZWEI Spalten und ZWEI Blöcke;
• diese VIER Zellen gehören NICHT zur Vorgabe;

      Avoidable Rectangle   I

DREI der vier Zellen des 'Avoidable Rectangle I' sind bereits mit den Kandidaten 'A' oder 'B' gelöst und nur in EINER Zelle muss mindestens ein zusätzlicher Kandidat 'x' vorhanden sein und so können in dieser EINEN Zelle beide Kandidaten 'AB' sicher ausgeschlossen werden:

000250080003001024000800001240065000900000003000140052800003000320500900090026000

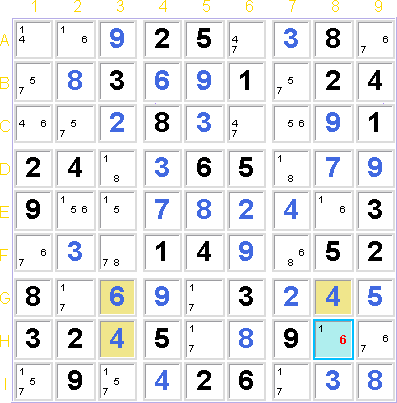
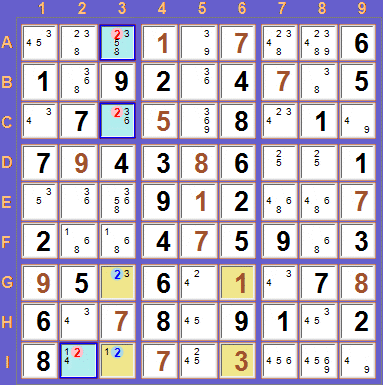
Beim Vorhandensein der Kandidaten '4' + '6' innerhalb der markierten Zellen, die nicht ein Teil der Vorgabe sind, würde ein Sudoku mit ZWEI Lösungen gebildet, was unmöglich ist.
   6 - 4        4 - 6
   4 - 6        6 - 4
Um diese Doppellösung innerhalb dieser VIER 'Avoidable Rectangle'-Zellen zu vermeiden, ist der Kandidat '6' in der hellblau markierten Zelle sicher auszuschließen, da NUR DORT zusätzliche Kandidaten vorhanden sind (hier nur Kandidat '1').

EINER dieser zusätzlichen Kandidaten (hier nur '1') muss in dieser Zelle 'H8' (hier hellblau markiert) vorhanden sein, damit ein eindeutiges Sudoku mit einer Lösung garantiert ist.

Dabei können auch nur EIN oder auch MEHRERE zusätzliche Kandidaten in dieser EINEN von VIER 'Avoidable Rectangle'-Zellen vorhanden sein.

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle I ... Beispiel A:



Beispiel mit Kandidatenpaar '37':

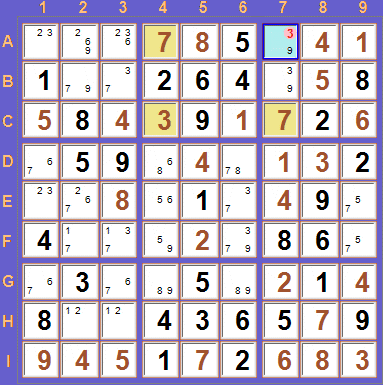
000005000100264008080090020059000002000010090400000860030050010800436509000102000

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle I ... Beispiel B:



Beispiel mit Kandidatenpaar '23':

090050000005201400000309000749000503300000007658000902000602000002904600080070000

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle I ... Beispiel C:



Beispiel mit Kandidatenpaar '18':

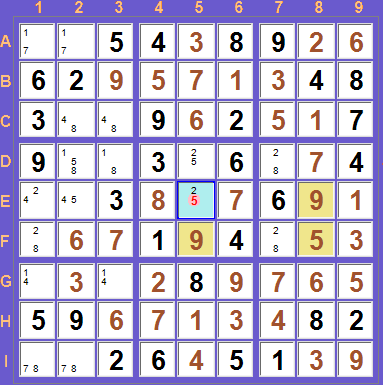
584000637006000500700000002043705120000030000015902870450000091002000300369000754

Top

      Avoidable Rectangle   II

ZWEI der vier Zellen des 'Avoidable Rectangle II' sind bereits mit den Kandidaten 'A' oder 'B' gelöst und nur in ZWEI Zellen innerhalb EINER Region sind jeweils einer der Kandidaten 'A' oder 'B' UND der GLEICHE zusätzliche Kandidat 'x' vorhanden und so kann im Schnittbereich dieser ZWEI Zellen dieser GLEICHE zusätzliche Kandidat 'x' außerhalb der VIER Zellen sicher ausgeschlossen werden:

000000000806209407430000062000617000000508000700942003900000008605403701007000300

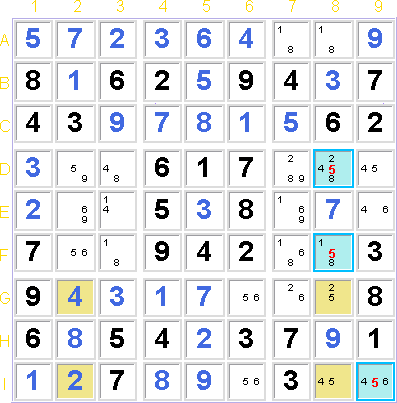
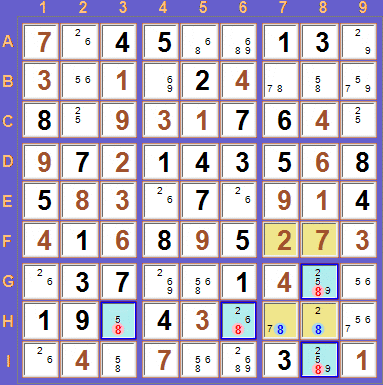
Beim Vorhandensein der Kandidaten '2' + '4' innerhalb der gelb markierten Zellen, die nicht ein Teil der Vorgabe sind, würde ein Sudoku mit ZWEI Lösungen gebildet, was unmöglich ist.
   4 - 2        2 - 4
   2 - 4        4 - 2
Um diese Doppellösung innerhalb dieser VIER 'Avoidable Rectangle'-Zellen zu vermeiden, muss in EINER der beiden ungelösten Zellen 'G8' oder 'I8' der zusätzliche Kandidat '5' enthalten sein, da NUR DORT (hier in 'G8' oder 'I8') EIN zusätzlicher GLEICHER Kandidat (hier '5') in diesem Ausschlussrechteck vorhanden ist.

Dies ergibt, das EINER dieser beiden '5' (hier in 'G8' oder 'I8') enthalten sein muss, damit ein eindeutiges Sudoku mit einer Lösung garantiert ist.

Das wir nicht wissen, welche der beiden '5' (hier in 'G8' oder 'I8') wahr ist, spielt hier keine Rolle!
So können also alle '5' im Schnittbereich dieser beiden definierten '5'er-Zellen (hier von 'G8' und 'I8') sicher ausgeschlossen werden.
(Also in allen Zellen, die von diesen beiden Zellen 'gesehen' werden (hier Spalte 8 und rechter unterer Block))

In diesem Beispiel kann also die '5' in den hellblau markierten Zellen sicher ausgeschlossen werden.

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle II ... Beispiel A:



Beispiel mit Kandidatenpaar '19':

005080400020000090304000502000871000801040603000326000708000105030000080002060300

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle II ... Beispiel B:



Beispiel mit Kandidatenpaar '27':

004500130000020000800007600070143508500070004010805000037001000190400000000000300

Top

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Avoidable Rectangle II ... Beispiel C:



Beispiel mit Kandidatenpaar '13':

000000006109204005070008010704306001000902000200405903050600070600809102800000000

Top